Değerli öğrenciler,
Matematiğin, öğrencilere zor gelmesinin en büyük nedenlerinden biri de ,matematiğin onlarca,yüzlerce formülden ibaretmiş gibi sanılması yada bilinmesi..Bu konuda ülkemizde matematik öğretim metodunda uygulanan sisteminde hatası olduğunu düşünüyorum…Gerçi liselerde yeni müfredatta bu eksiklik az da olsa giderildi ama bir türlü müfredatın istediği tarzda ders sunumuna geçiş yapamadık…Zaten bu o kadar da kolay olacağa benzemiyor..Hayırlısı bakalım..
Matematik büyük oranda mantık işi..Elbette zaman zaman, formül kullanmak işi kolaylaştırır ama, konuyu formül temelli anlatmak,işi daha da zor ve zor sıkıcı hale getirir.Bu yüzden de, direk formülle çözülen soruları pek sevmem…
Matematiğin en önemli konularından olan (Çünkü LYS de en çok soru sorulan konulardan biri) trigonometri konusunun, zor gibi görülmesinin en önemli nedenlerinden biri de, kitaplarda sayfaları dolduran formüller…
Ben burada trigonometri konusunu baştan başlayıp, sonuna kadar anlatmayacağım.Bu da zaten bir yazı ile mümkün değil.Ama bu konunun en önemli bölümünü, bir sürü formüle mahkum kalmadan,nasıl hallederiz? Bu soruya cevap vermeye çalışacağım.Eğer anlatabilirsem,cümleleri uzatmadan,siz de dikkatli takip ederseniz,çoğunuzdan kesinlikle dua alacağım,en büyük şifa de benim için bu….Bakmayın kitaplarda bir yığın formül olduğuna….
ONLARCA FORMÜLE BAY BAY!
Gelelim artık,bu konunun her yerinde karşımıza çıkacak olan, ilgili bölümdeki formüllerden kurtulmanın püf noktasına:
Birinci bölgede yer alan,30,45,60 gibi oranları 9.sınıfta öğrendiniz.Ve muhtemelen 11.sınıfta ders öğretmeni,trigonometri konusunda bir kez daha bunları tekrar etmiştir.Öncelikle sinüs ve kosinüs eksenlerinde yer alan 0,90,180,270,360 açıların ve 30,60 ve 45 açıların trigonometrik oranlarını çok çok iyi bilmeliyiz.Bunları çok iyi öğrendikten sonra, gerisi çorap söküğü gibi inanın,bütün mesele işin püf noktasını kavrayabilmek yada kavratabilmek…
Şimdi sizlere,2.3.yada 4.bölgede yer alan 135,120,225,315 vb…açıların oranlarını bulurken izleyeceğimiz yöntemi kısa ve öz anlatıp,onlarca formülü ezberlemeden,trigonometri konusunun en önemli bölümünü halletmiş olacağız...Gerisi inanın oldukça kolay…Ve bir o kadar zevkli…:)
Resimdeki formüllerin yer aldığı resmi,11.Sınıf Matematik Ders Kitabından (Sayfa-168) aldım.Bu formüller Sayfa 164-168 de yer alıyor.Yani aşağıda özetleyeceğim mantık, ders kitabında tam 5 sayfa…Palme’nin konu anlatımında daha çok sayfa…Lüzumsuz mu? kesinlikle değil..Benim demek istediğim,bu kadar sayfalar dolusu formülü ezberlemek zorunda olduğunuzu sanmayın,hiç gerek yok…Burada formüllerle ilgili kurala götüren ispata,nedene değinemeyeceğim.Çünkü bu ayrı bir ders konusu.Muhtemelen öğretmen arkadaşlarım derste o mantığı anlatmışlardır.Ben, sadece sonucun kuralını izah ederek, formüllere nasıl bay bay diyebiliriz, onu anlatacağım…
Uzattım ama değeceğini düşünüyorum,çok az kaldı.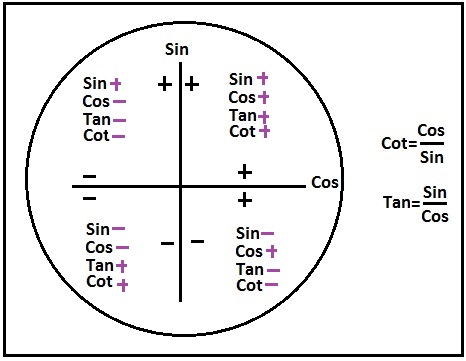 Şimdi şunu da söyleyeyim:Bölgelerde trigonometrik değerlerin işaretini mutlaka çok iyi bilmeliyiz.Şimdi resimde görüldüğü gibi,analitik düzlemdeki y ekseni sinüs ekseni,x ekseni kosinüs ekseni.Sinüs ve Kosinüs’ün işaretini bu eksenlere göre belirliyoruz.
Şimdi şunu da söyleyeyim:Bölgelerde trigonometrik değerlerin işaretini mutlaka çok iyi bilmeliyiz.Şimdi resimde görüldüğü gibi,analitik düzlemdeki y ekseni sinüs ekseni,x ekseni kosinüs ekseni.Sinüs ve Kosinüs’ün işaretini bu eksenlere göre belirliyoruz.
Tan ve Cot ise bunların bölümüne eşit olduğu için,sinüs ve kosinüs’ün zıt olduğu 2.ve 4.bölgede negatif,aynı işaretli olduğu 1.ve 3.bölgede pozitif.
GENİŞ AÇILARIN TRİGONOMETRİK ORANLARINDA PÜF NOKTA
Gelelim asıl konumuza,
1.bölgedeki 30,45,60 gibi açıların oranlarını zaten biliyoruz,bilmek zorundayız.Ve 1.bölgede tüm trigonometrik oranlar pozitif.
Diğer bölgelerde yer alan tüm açıların oranlarını bulurken 1.bölgedeki açı(lar) kullanılır.Çoğunlukla da 30,45 ve 60 kullanılır.
Cos120 =? Sin215=? tan 315=? vb….
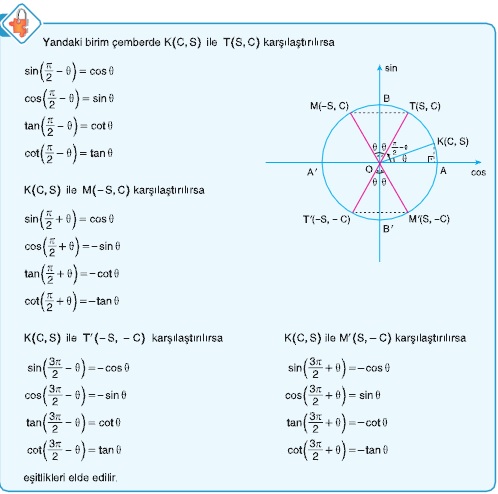
Bu oranları bulurken,bu açıları iki türlü elde edebiliriz.Örneğin 120=90+30 veya 120=180-60,benzer şekilde 315=370+45 veya 315=360-45 şeklinde.
Bu açıların oranlarını bulurken işaretini belirledikten sonra,bu iki eşitlikten istediğimizi kullanabiliriz.Ancak eğer ;180 veya 360 kullanılırsa oran değişmez,90 veya 270 kullanılırsa trigonometrik oran Sin—Cos,Tan–Cot şeklinde değişir.
Şimdi 120’nin oranlarını iki şekilde de bulmaya çalışalım ve sonucun değişmediğini görelim.
Cos120 (2.bölgede olduğu için işareti – ) Cos120=– Cos(90+30)=– Sin30= – 1/2 , Cos120= – 1/2 (90 kullanıldığı için cos,sin oldu)
Cos120=– Cos(180-60)=– Cos60= – 1/2 , Cos120= – 1/2 (180 kullanıldığı için oran değişmedi)
Her iki durumda da önce Cos120’nin işaretini belirledik.
Bu kadar,bu kuralı bilin yeter,formüle falan hiç gerek yok…Artık bunu istediğiniz açıya uygulayın…
“Müjdeleyin, nefret ettirmeyin; kolaylaştırın, zorlaştırmayın.” –Hadis-i Şerif
Ali SANCI-Matematik Öğretmeni
Çorum Anadolu Lisesi











Elinize Sağlık hocam. Rab’bim sizin sıkıntılarınızı kaldırsın..
Olayi cidden cok guzel anlatmissiniz cok tesekkur ederim harikasniz
Hocam öncelikle bu sade ve güzel üslupunuzdan dolayı sizlere teşekkür etmek istiyorum.
Bu konuyu internet üzerinde farklı hocalardan dinlememe rağmen bu kadar saf ve öz anlatan birisinden bir çırpıda anladığımı farkettim… Allah sizden razı olsun
[…] çözmeden önce,eğer bu konuyu gerçekten çok iyi öğrenmek istiyorsanız “Trigonometrik değerleri bulurken onlarca formülü ezberlemeye son!” başlıklı yazıyı okumanızı […]
Teşekkür ederim.
Emeğinize sağlık hocam