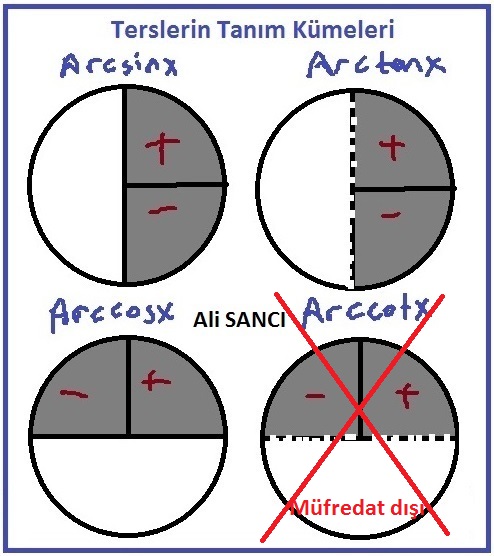
Trigonometrik fonksiyonları anladıysanız tersleri o kadar kolay ki..Tek bilinmesi gereken terslerin tanım kümeleri..Bunu da aşağıda şekle dökerek daha kolay hatırlanabilir hale getirmeye çalıştım….
Trigonometrik fonksiyonların tersi olan arcsinx,arccosx,arctanx ifadeleri ile ilgili soruların çözümünde takılmamanız için (buraya kadar olan konuları iyi bilmeniz gerekiyor tabi,bir oran verildiğinde diğerinin bulunması,bölgelerde trigonometrik fonksiyonların işareti vb..) ters fonksiyonların tanım kümelerini şu şekilde ifade edersek daha kolay hatırlanacağını düşünüyorum.
Merhaba sayın hocam ben trigonometri konusunu çok seviyorum ama bir o kadar da bu konuyu hiç anlayamıyorum ve anlamakta oldukça zorluk çekiyorum ama anlayamadım diye asla pes etmedim ve pes etmeyi hiç düşünmüyorum.sizden ricam ben bu konuyu nasıl anlarım en kısa yoldan nasıl kavrarım bana lütfen yardımcı olabilirmisiniz.
–Konuyu nasıl anlayacağım
–öğrenirken hangi ana blokları öğreneceğim
– öğrenirken hangi blokları öğreneceğim
–trigonometri ye nasıl bir giriş yapacağım
–bölgeleri açıları nasıl anlayacağım
–derece radyan grand nasıl anlayacağım
–sinüs kosinüs tanjant ve kotanjant her birini her bi bölgede nasıl kavrayacağım
–oranlar nasıl ortaya çıkıyor tersi nasıl oluyor
–konuyu tablo üstünde nasıl anlayacağım
–konuyu grafik üstünde nasıl anlayacağım
–formülleri nasıl kavrayacağım
Lütfen allah rızası için bana yardımcı olabilirmisiniz hocam?
Bu sorunun cevabını şöyle özetleyeyim,zaten maddeler için söylenecekler aynı hemen hemen.
Temelden işin özünü çok iyi anlayın.Mesela 45’in oranları nereden geliyor.135’in oranları için sadece 45’i ve birde bölgelerin işaretlerini bilmek yeterli.Formülleri birbirinden bağımsız ezberlemeyin.Ezberleyin ancak nereden geldiğini bilin.Kısaca bilgiler kendi öz malınız olmalı.tanx.cotx=1 neden 1? Ayrıca şunu da söyleyeyim;Biraz da mevcut kitaplar konuyu gereksiz formüllerle uzatıyorlar.Mesela dönüşüm formülleri diye başlık görürsünüz ve 1-2 sayfa formül yazarlar.Halbuki o formüller yerine işin kuralı olan;360,180 açılarına ekleme çıkarmada değişmediği,90 ile 270 de değiştiği bir de işaretin bölgelere göre belirlendiği bilinirse hiç ezbere gerek yok.Hepsi de bu kuraldan çıkıyor zaten.İşaret olayı da analitik düzlemdeki apsis ve ordinat gibi.Çünkü (x,y)=(cos,sin).Dolaysıyla trigonometrik değerlerin işaretinin de (x,y) nin işareti ile aynı olduğunu bilenin ezber diye bir derdi yok.
Kısaca konuları birbirinize zincirleme bağlamak gerekir.Zaten beyin bilgileri birbirine bağlayınca asla unutmaz.Hafızamızın çalışma şekli bize bilgileri birbirine bağlayarak öğrenmemiz gerektiğini söylüyor.Şu an aslında okullarda, tam da bu şekilde bir öğretim yapamıyoruz.Konuları bitirebilmek için, bir de öğrenciler sıkılmasın diye konuların çok detayına,özüne girmeden hızlıca geçiyoruz.Ben bir çok konuda detaylı anlatmayı deniyorum kalıcı ve iyi bir öğrenme olsun diye maalesef öğrencileri bir türlü konuya çekemiyorum.Ama yine de becerebildiğim ölçüde bu konuda ısrar ediyorum.Bu da ilkokul,ortaokuldan gelen alışkanlıkların devam ediyor olmasından dolayı.
Şimdilik aklıma gelenler bunlar.Bu sorunun cevabı aslında uzun bir yazı konusu.Bu gün 9.sınıf matematik trigonometri-2 konusu ile ilgili bir video yayına alacağım.İsterseniz bir dinleyin.Belki az da olsa ışık tutar.Tabi 9.sınıflar için anlatacağım için çok ayrıntıya girmeyeceğim.
–Problemlerde takip edilecek kurallar nelerdir
Benim görüşüm;problemler birikim işi.Ayrıca bilgileri pratik kullanma yeteneği ile de ilgili.Ama somut olarak şunu söyleyebilirim:Geometri konuları gibi problemler için de bol bol soru çözmek şart.Tabi önce bir kaç çözümlü fasikül bitirdikten sonra.Bu konuda mustafa yağcı’nın problemlerin olduğu kaynağı alabilirseniz size çok faydası olacak.Çünkü temelden anlatıyor.Ezbere değil işin mantığını sunarak adım adım ilerliyor kitap.
Konu anlatım fasikülü bitirince bir kaç tane soru fasikülü bitirmelisiniz.Problemlerin kısa sürede bitmeyeceğini belirteyim.Bu nedenle ben hep 11.sınıf öğrencilerine yaz tatilinde geometri ve problemleri bitirmelerini öneriyorum.Diğer konuların bir sınırı var..Ama bu iki konunun bitmesi kolay değil…Bir de biraz olasılık zaman isteyen bir konu…